Stability of an Annular Combustion Chamber
In section 4.2 of [DSZ] the problem of stability of an annular combustion chamber was used as a test case for their rootfinding algorthim. The problem consisted of finding all the zeros of the holomorphic function
with constants
The result there can be replicated in cxroots with:
from numpy import exp
from cxroots import Rectangle
A = -0.19435
B = 1000.41
C = 522463
T = 0.005
f = lambda z: z**2 + A*z + B*exp(-T*z) + C
df = lambda z: 2*z + A - B*T*exp(-T*z)
rectangle = Rectangle([-15000,5000], [-15000,15000])
roots = rectangle.roots(f, df, root_err_tol=1e-6)
roots.show()
(Source code, png, hires.png, pdf)
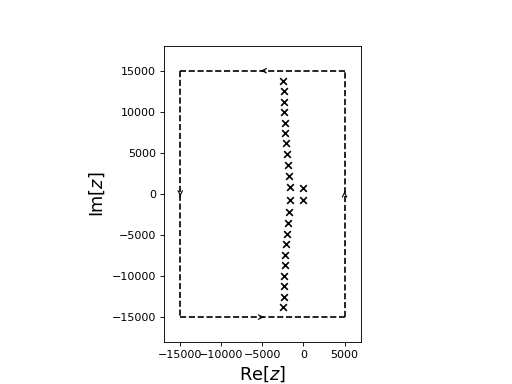
Note that if root_err_tol=1e-6 is omitted then the Newton-Raphson method used to refine the roots is sometimes unable to converge to a point where \(|f(z)|<\text{root_err_tol}\). In this case the contour bounding the root is continually subdivided until it has area less than newton_step_tol at which point the best approximation to the root within the contour will be taken to be ‘good enough’ and a warning message will be printed to inform the user.
References
“Locating all the Zeros of an Analytic Function in one Complex Variable” M. Dellnitz, O. Schütze, Q. Zheng, J. Compu. and App. Math. (2002), Vol. 138, Issue 2