Using Known Roots or Symmetries

Guessing Roots

The guess_roots argument of Contour.roots can be used to supply any roots the user already knows or suspects. For example, suppose we want to find the roots of the function

\[f(z)=(z+1.2)(z-2.5)^2\left(e^{-z}\sin\left(\frac{z}{2}\right)-1.2\cos(z)\right)\,, \quad |z|<3\]

It’s obvious that 2.5 and -1.2 are roots so we can tell cxroots this by passing guess_roots=[2.5, -1.2] to C.roots().

from numpy import exp, sin, cos
from cxroots import Circle
C = Circle(0, 3)
f = lambda z: (exp(-z)*sin(z/2)-1.2*cos(z))*(z+1.2)*(z-2.5)**2
C.roots(f, guess_roots=[2.5, -1.2])

This causes cxroots to first check for roots within small circles centered on the points 2.5 and -1.2

(Source code)

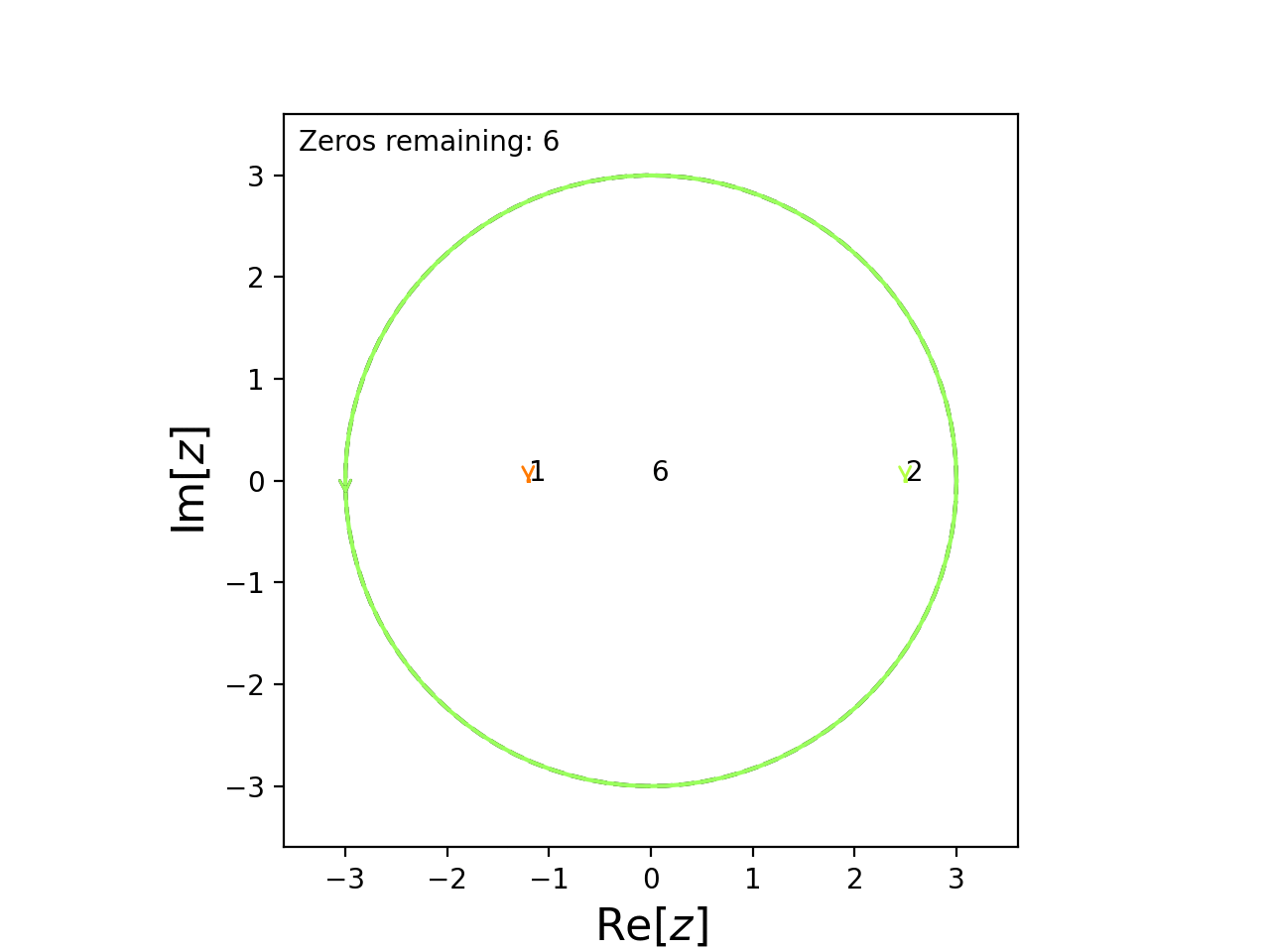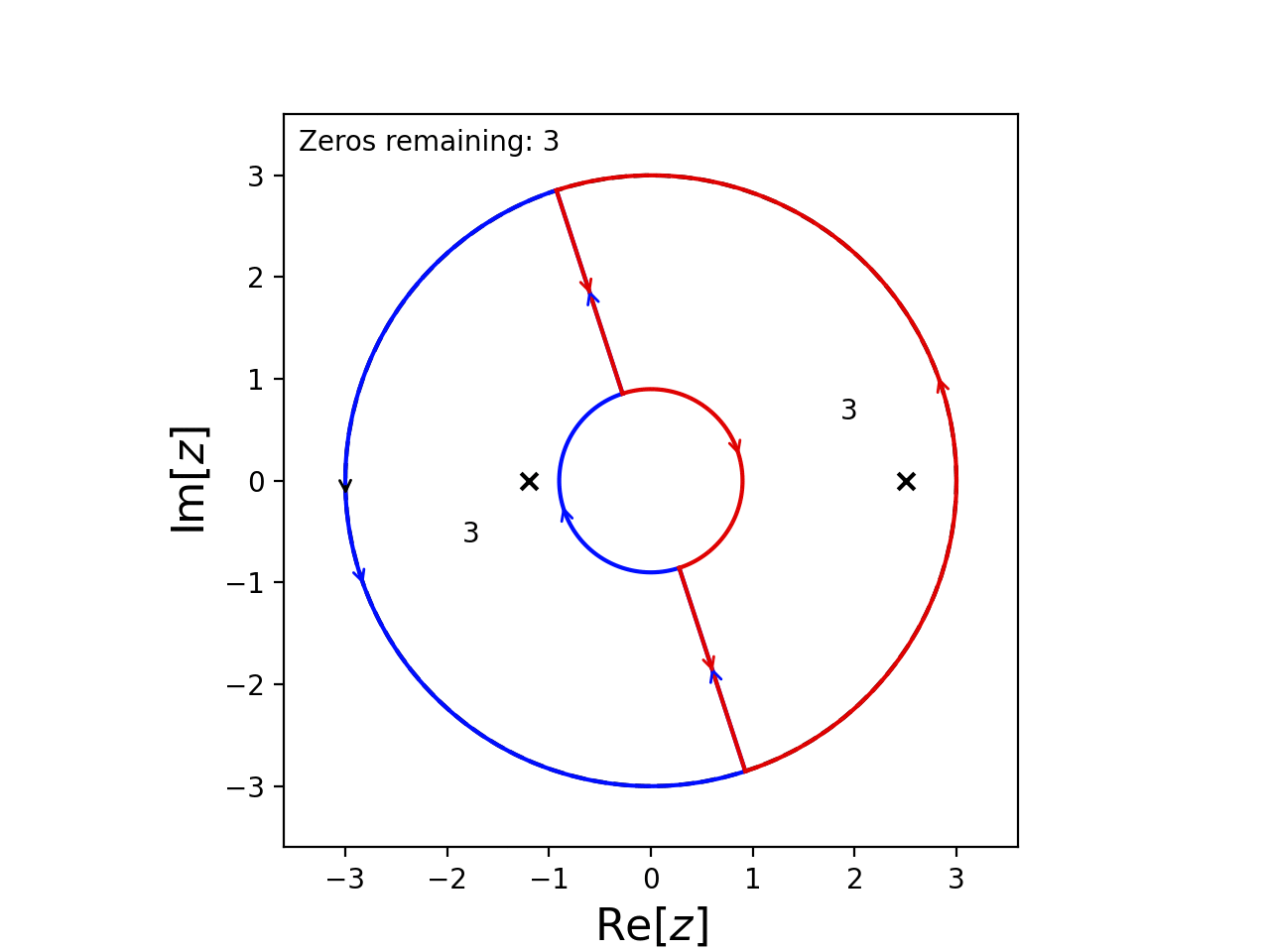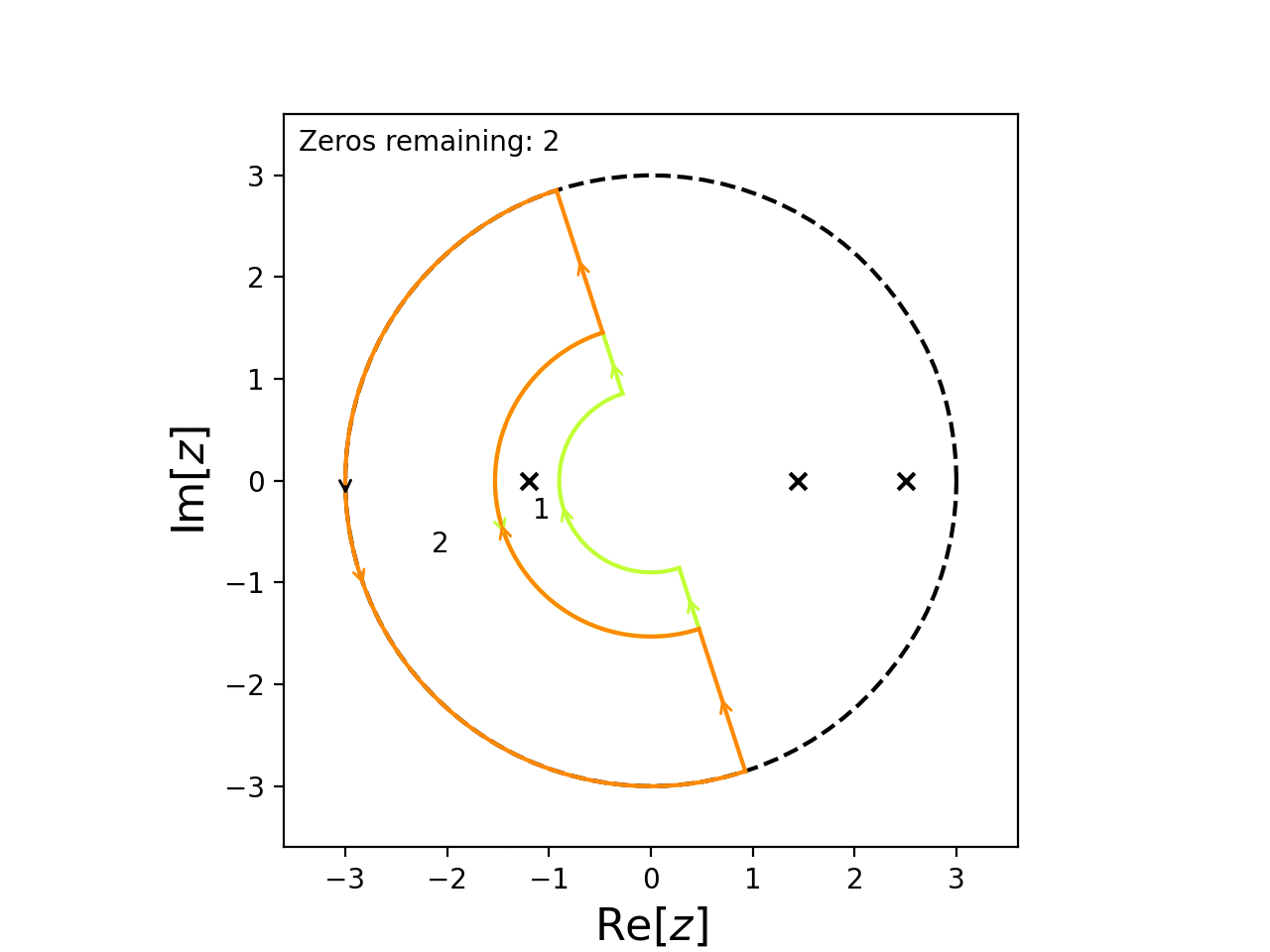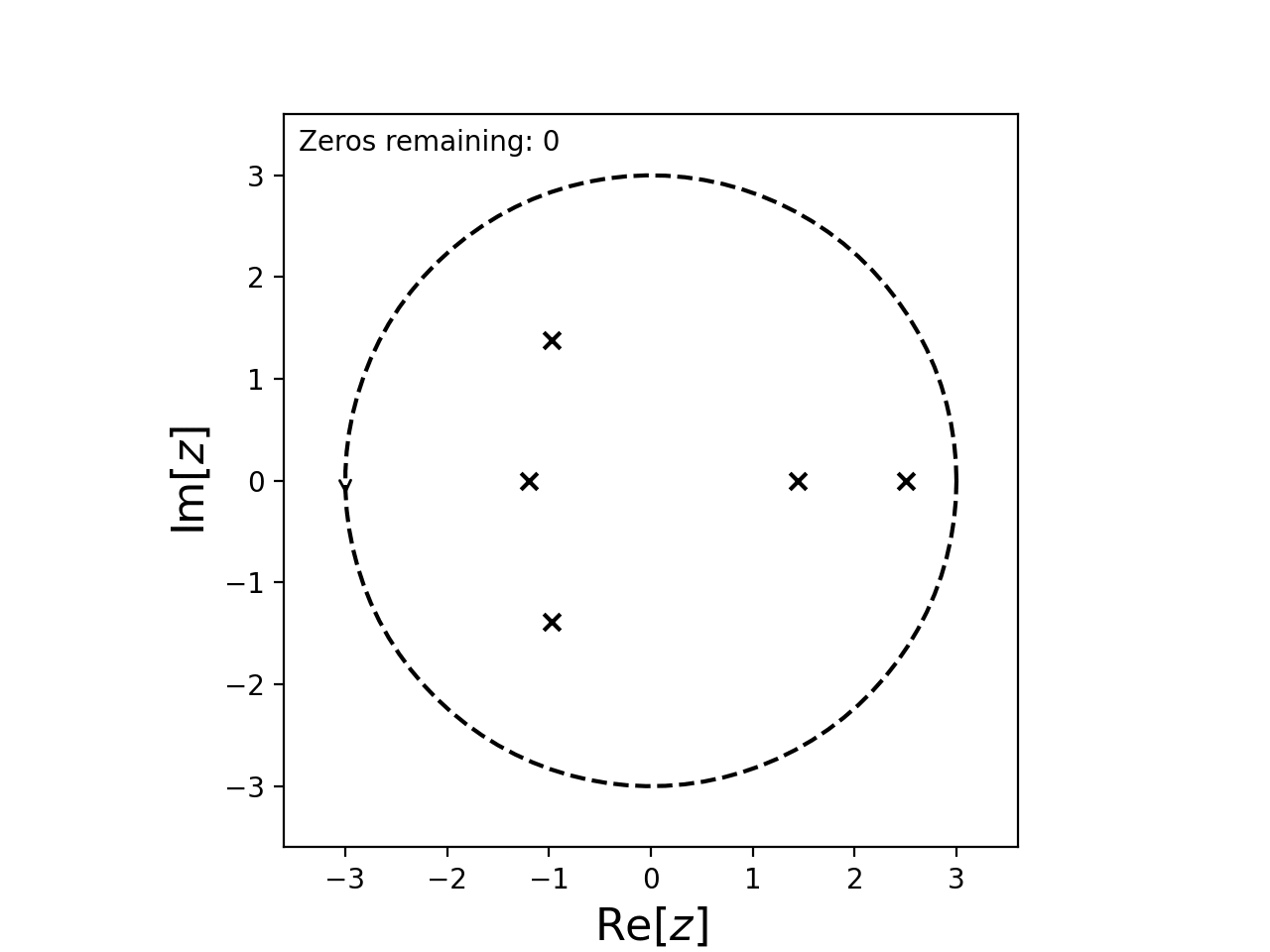
_images/guess_roots.gif

Note that the list we supply to guess_roots simply tells cxroots where to look first for roots, the guesses will not be blindly accepted so they do not need to be particularly accurate.

Guessing Root Symmetry

It may be that something is known about the structure of the roots. cxroots can be told this using the guess_roots_symmetry argument which should be a function of a complex number, \(z\), which returns a list of roots assuming that \(z\) is a root.

For example, if \(z_i\) is a root of

\[f(z)=z^{26}-2z^{10}+\frac{1}{2}z^6-1\]

then so is \(\overline{z_i}\) and \(-z_i\). We should therefore pass guess_roots_symmetry=lambda z: [z.conjugate(), -z] to C.roots()

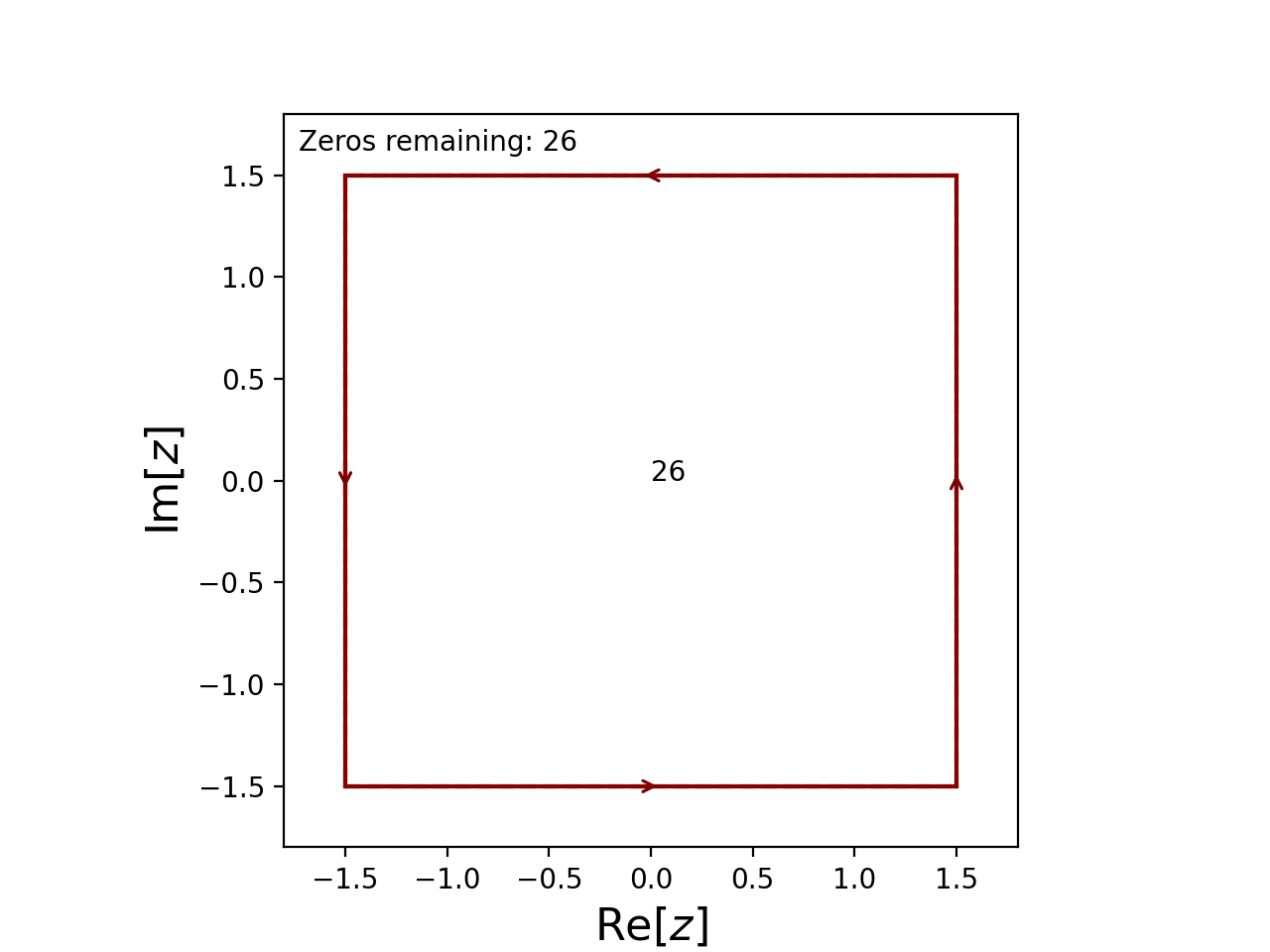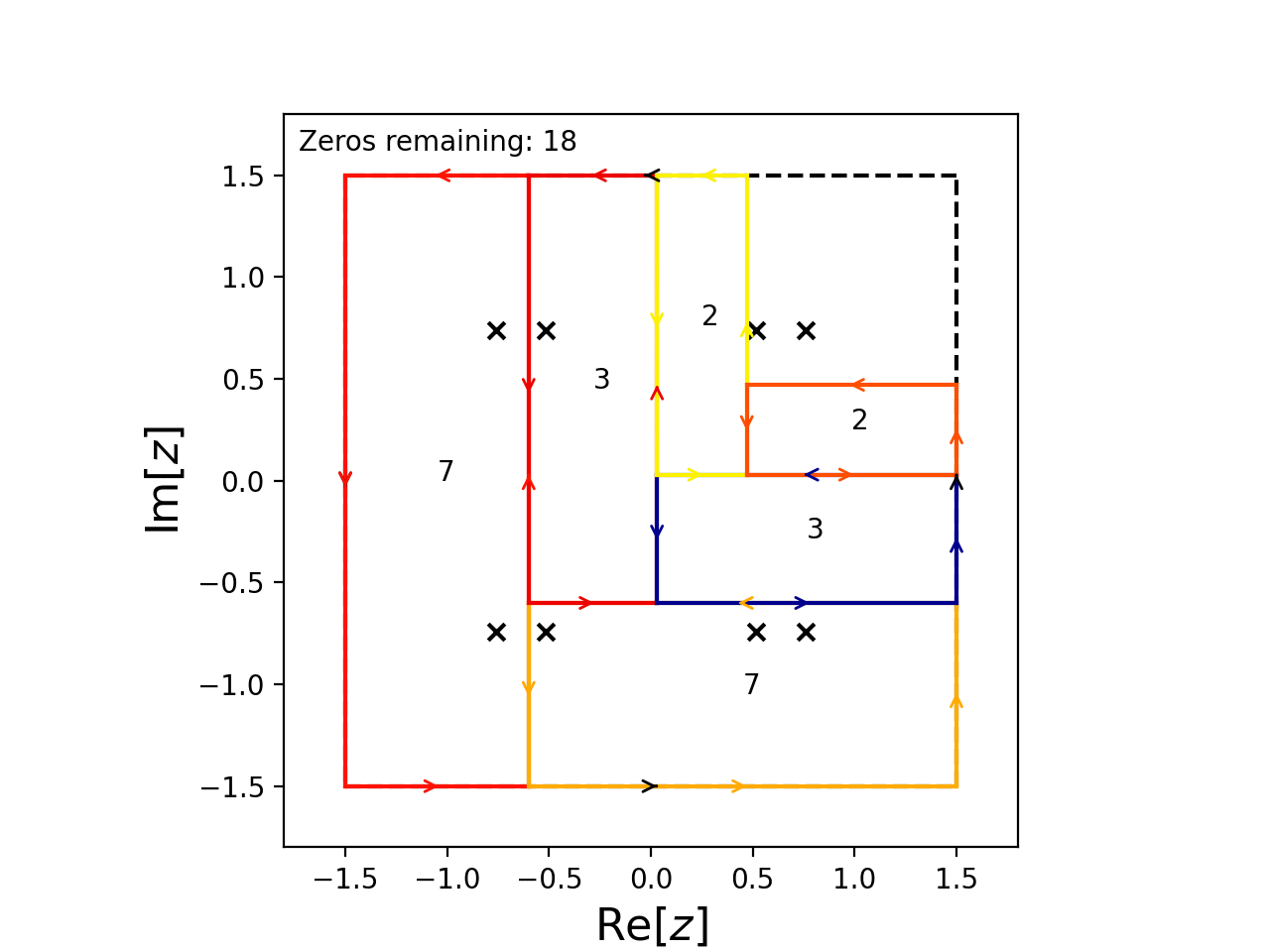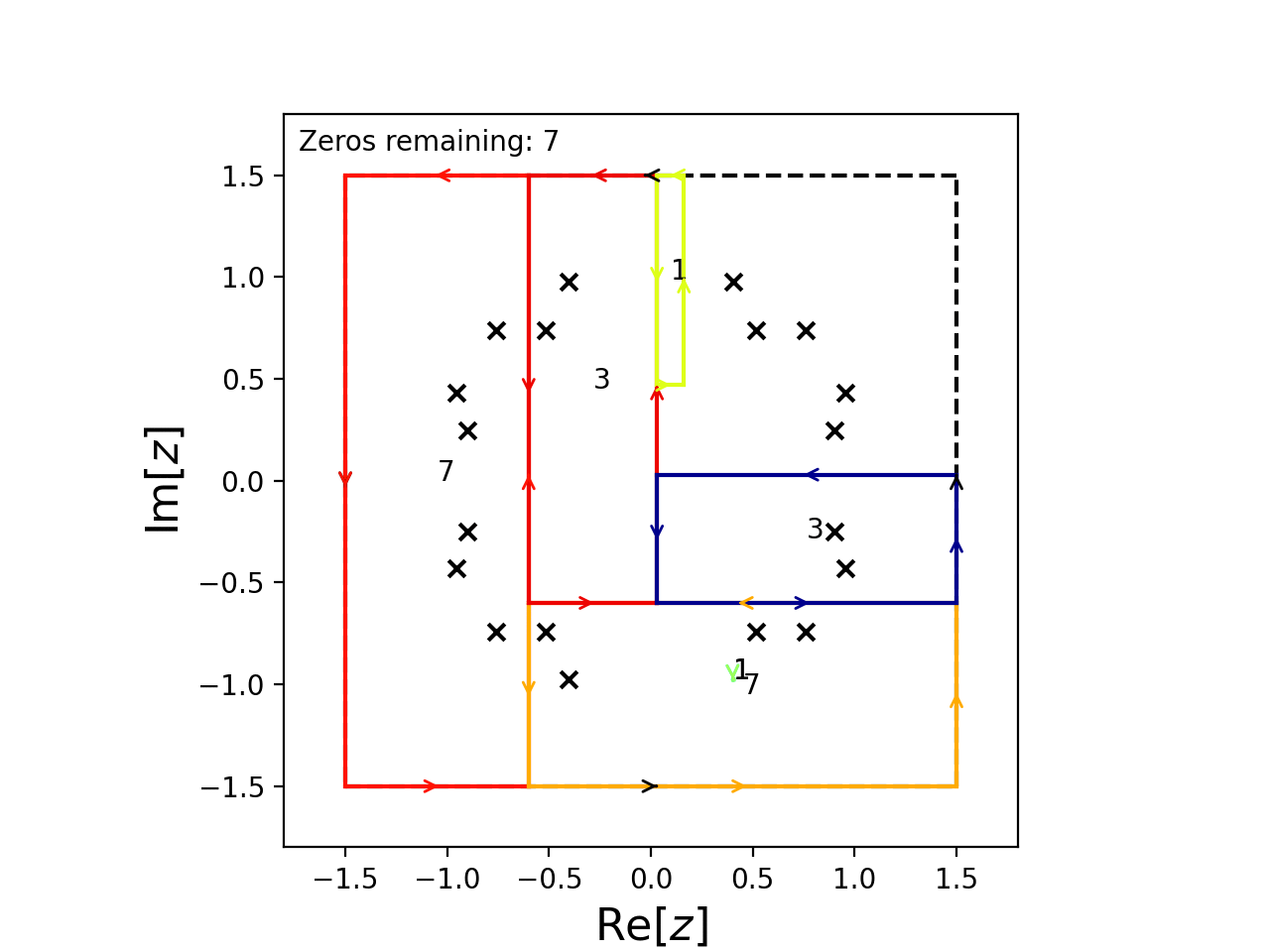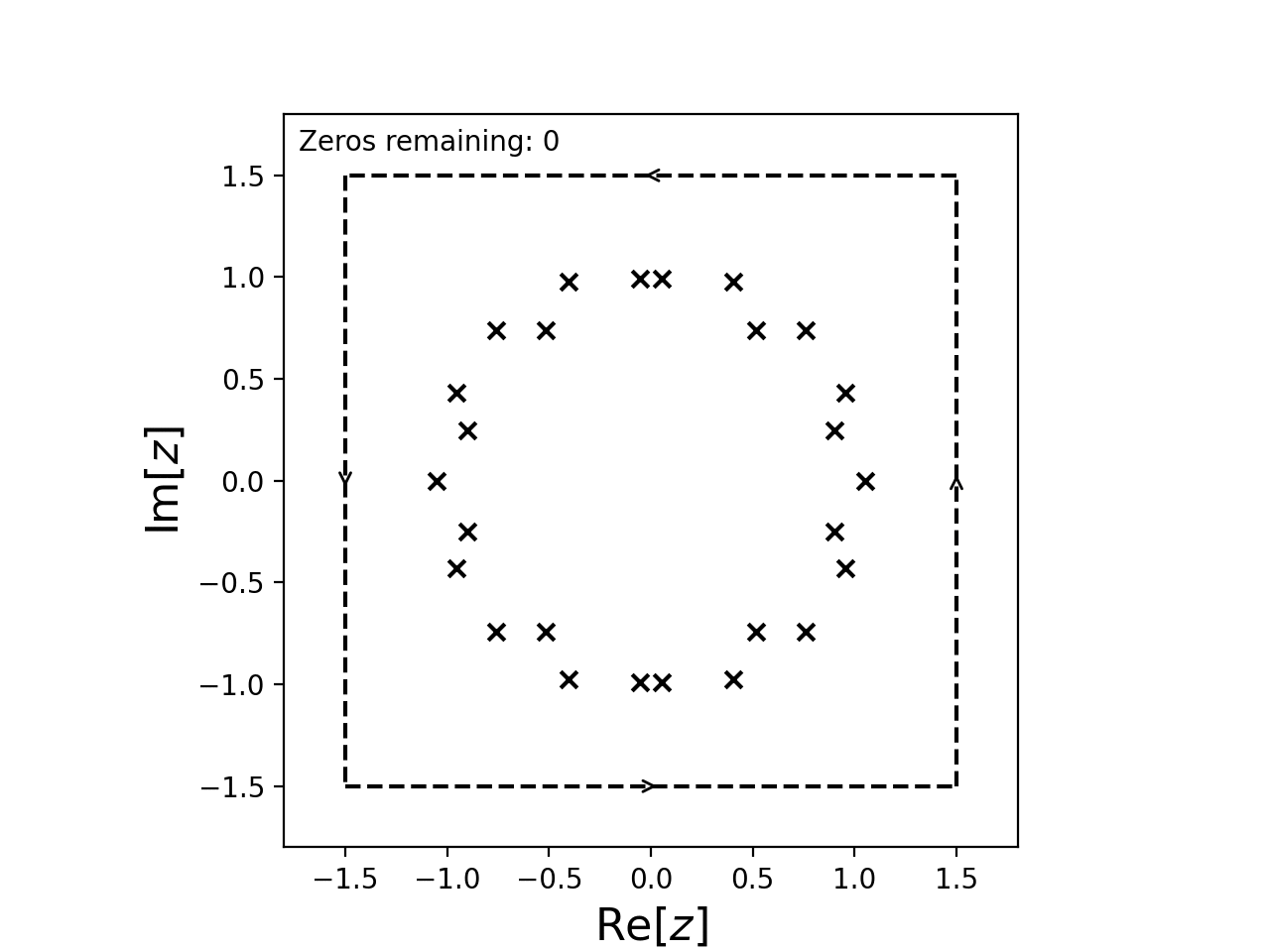
from cxroots import Rectangle
C = Rectangle([-1.5,1.5], [-1.5,1.5])
f  = lambda z: z**26-2*z**10+0.5*z**6-1
df = lambda z: 26*z**25-20*z**9+3*z**5
C.roots(f, df, guess_roots_symmetry=lambda z: [z.conjugate(), -z])

This causes cxroots to check for roots within a small circle centered on the points \(\overline{z_i}\) and \(-z_i\) whenever a root, \(z_i\), is found.

(Source code)

_images/ex_rootSymmetry.gif