cxroots: rootfinding for complex analytic functions
cxroots is a Python package for finding all the roots of a function, \(f(z)\), of a single complex variable within a given contour, \(C\), in the complex plane. It requires only that both:
\(f(z)\) has no roots or poles on \(C\)
\(f(z)\) is analytic in the interior of \(C\)
The implementation is primarily based on Kravanja and Van Barel [KVanBarel00] and evaluates contour integrals involving \(f(z)\) and its derivative \(f'(z)\) to approximate the roots. Then iterative methods, such as Newton-Raphson or Muller’s method are used to refine the roots. If \(f'(z)\) is not provided then it is approximated. See the Theory page for a more detailed explanation.
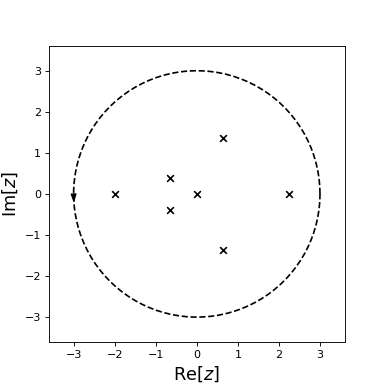
from numpy import exp, cos, sin
f = lambda z: (exp(2*z)*cos(z)-1-sin(z)+z**5)*(z*(z+2))**2
from cxroots import Circle
C = Circle(0,3)
roots = C.roots(f)
roots.show()
Documentation
Getting Started
User Guides